Authors: Ismail Elezi, Sebastiano Vascon, Alessandro Torcinovich, Marcello Pelillo, and Laura Leal-Taixé
Abstract: Deep metric learning has yielded impressive results in tasks such as clustering and image retrieval by leveraging neural networks to obtain highly discriminative feature embeddings, which can be used to group samples into different classes. Much research has been devoted to the design of smart loss functions or data mining strategies for training such networks. Most methods consider only pairs or triplets of samples within a mini-batch to compute the loss function, which is commonly based on the distance between embeddings. We propose Group Loss, a loss function based on a differentiable label-propagation method that enforces embedding similarity across {\it all} samples of a group while promoting, at the same time, low-density regions amongst data points belonging to different groups. Guided by the smoothness assumption that “similar objects should belong to the same group”, the proposed loss trains the neural network for a classification task, enforcing a consistent labelling amongst samples within a class. We show state-of-the-art results on clustering and image retrieval on several datasets, and show the potential of our method when combined with other techniques such as ensembles.
Introduction
Deep metric learning is the task of obtaining good features that can be later used for clustering and image retrieval. Neural networks used for this task are collectively known as Siamese Neural Networks. While at first look the problem looks similar to that of image classification, there are two important differences. First, the inference is done in classes of images that are not present during the training of the neural network. Second, typically the number of images per class is much lower than in the task of image classification. Thus, training a network in the task of classification, and using the same network to produce features for clustering or retrieval typically results in unsatisfying performances.
To mitigate these issues, many researchers have worked on different loss functions. The main idea of all of deep metric embedding loss functions is to formulate the loss function not as a function of features for each individual image, but as a function of relations between the produced features. For example, the contrastive loss function (the original loss for Siamese Neural Networks) takes into consideration a pair of images, and it tries to minimize the Euclidean distance between the features of them providing that the images come from the same class, otherwise it maximizes their distance. The most famous loss function for Siamese Networks is the triplet loss. The triplet loss works similarly to contrastive loss, but instead of considering a pair of images, it considers a triplet of images, containing an anchor, a positive and a negative image (with the anchor and positive being from the same class, while the negative being from a different class). The loss tries to minimize the Euclidean distance between the anchor and the positive (in embedding space) while maximizing the distance between the anchor and the negative. To make either of these two losses work well, in practice, a collection of tricks is needed (hard-negative mining, intelligent sampling or multi-task learning). Furthermore, in a mini-batch of size n despite that the number of pairwise relations between samples is O(n^2), contrastive loss uses only O(n/2) pairwise relations, while triplet loss uses O(2n/3) relations.
We advocate that we can bypass the use of such tricks by adopting a loss function that exploits, in a principled way, the global structure of the embedding space, and at the same time uses all O(n/2) pairwise relations. In this work, we propose a novel loss function for deep metric learning, called the Group Loss, which considers the similarity between all samples in a mini-batch. To create the mini-batch, we sample from a fixed number of classes, with samples coming from a class forming a group. Thus, each mini-batch consists of several randomly chosen groups, and each group has a fixed number of samples. An iterative, fully-differentiable label propagation algorithm is then used to build feature embeddings which are similar for samples belonging to the same group, and dissimilar otherwise.
Methodology
As we explained in the previous section, most loss functions used for deep metric learning do not use a classification loss function, e.g., cross-entropy, but rather a loss function based on embedding distance. The rationale behind it is that what matters for a classification network is that the output is correct, not that the embeddings of samples belonging to the same class are similar. Since each sample is classified independently, it is entirely possible that two images of the same class have two distant embeddings that both allow for correct classification. We argue that a classification loss can still be used for deep metric learning, if the decisions do not happen independently for each sample, but rather jointly for a whole group, i.e., the set of images of the same class in a mini-batch. This is the goal of Group Loss, to take into consideration the global structure of a mini-batch. To achieve this, we propose an iterative procedure that refines the local information, given by the softmax layer of a neural network, with the global information of the mini-batch, given by the similarity between embeddings. This iterative procedure categorizes samples into different groups and enforces consistent labeling among the samples of a group. While softmax cross-entropy loss judges each sample in isolation, the Group Loss jointly takes into consideration all the samples in a mini-batch.
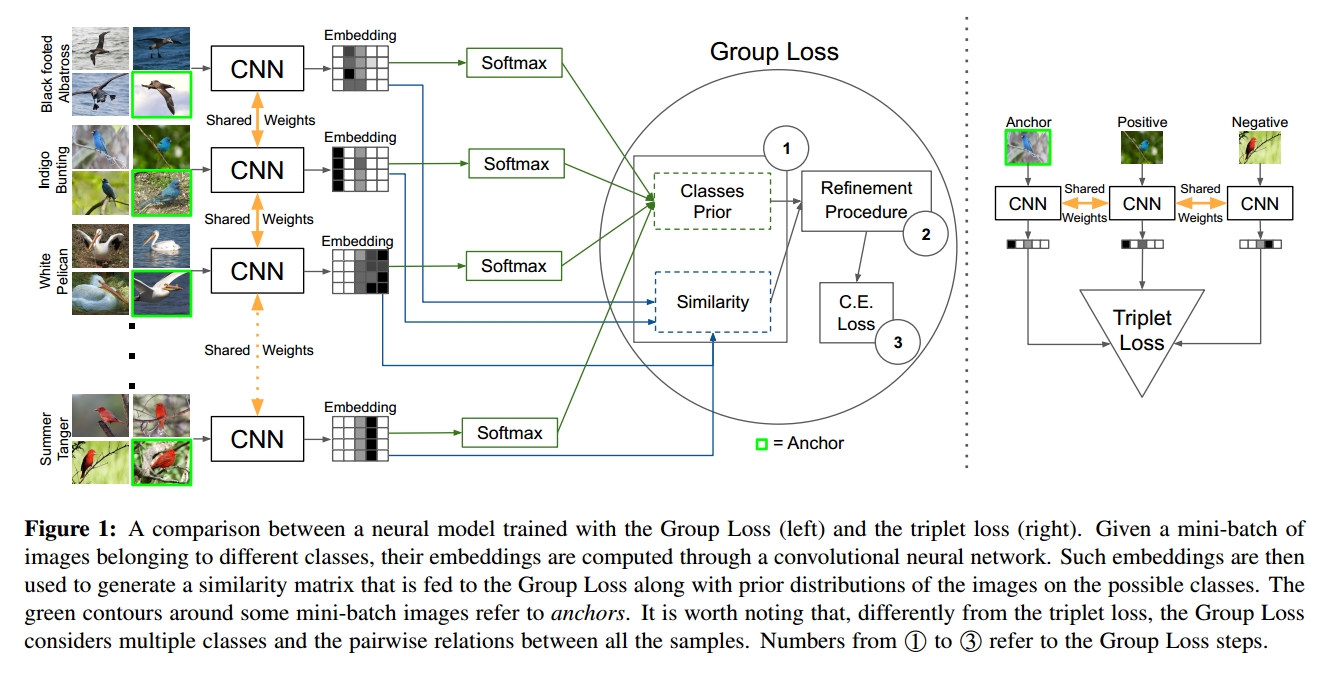
Given a mini-batch B consisting of n images, we consider the problem of assigning a class label to each image in B. The method needs a matrix of soft-label assignment for each image (computed via the softmax layer of a CNN) and a matrix of similarity W coding the similarity between the images. The high-level description of the method is as follows:
1) Initialization: Initialize X, the image-label assignment using the softmax outputs of the neural network. Compute the n×n pairwise similarity matrix W using the neural network embedding.
2) Refinement: Iteratively, refine X considering the similarities between all the mini-batch images, as encoded in W, as well as their labeling preferences.
3) Loss computation: Compute the cross-entropy loss of the refined probabilities and update the weights of the neural network using backpropagation.
The initialization of the matrices W and X is straightforward. For the matrix W, we choose the correlation between features as similarity metric, however, other metrics can be used (such as a Gaussian kernel). For the initial matrix of probabilities, we use the outputs of the softmax layer of the network. Furthermore, for a few (randomly chosen) samples, we replace the softmax initialization with one-hot labeling. We call these samples “anchors”.
Step (2) is the core of this work and is needed to update the matrix of probability X, based on the similarity between samples in the mini-batch. We use a dynamic system based on replicator dynamics. At each step of the dynamical system, the matrix X is affected from the matrix W. If two samples a and b are similar (their pairwise entry in W is high), then they will heavily affect each other. So on the first step of the dynamical system, each sample affects each other (some more, some less, based on their similarity). On the second step, the same happens but now each sample is already affected by all the other samples in the mini-batch, and so the system is considering higher-order information between samples. The system is guaranteed to converge after a number of iterations, although for implementation purposes we decide the number of steps in advance (we get the best results when we use 1-3 steps). A high-level illustration of the system is given in the image below:
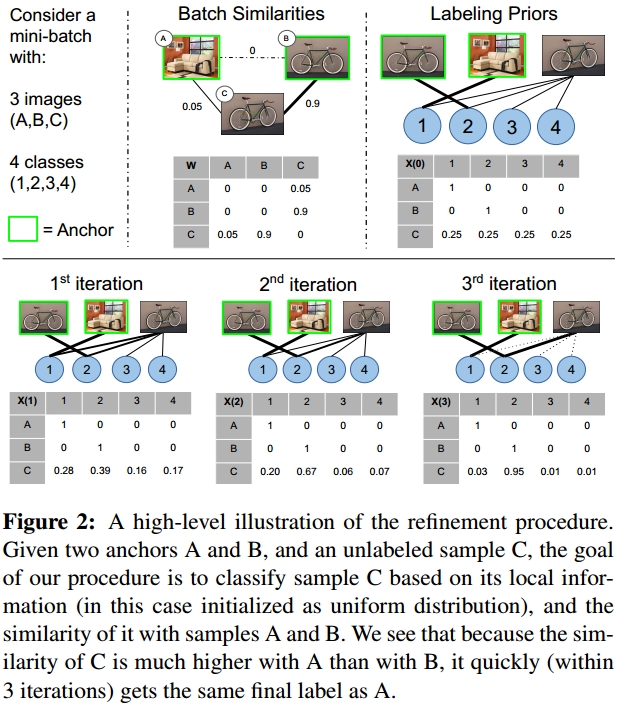
The system might remind other dynamical systems like message-passing networks (MPN), conditional random fields (CRF) or relaxation labeling systems. It has nice mathematical properties and the convergence is guaranteed. We give the mathematical details in section 3.3 of the main paper.
Finally, after the refinement procedure, the new matrix of label assignment is evaluated in Step (3). In this work, we use the cross-entropy loss function and update the weights of the network via the backpropagation algorithm (using PyTorch auto-differentiation library).
Results
Our method reaches state-of-the-art results, outperforming every other loss function by a large margin in 3 public datasets and 2 evaluation metrics (Recall and Normalized Mutual Information). Furthermore, we show that the loss function can be combined with a naive ensemble (created by training N neural networks independently in the same task) to outperform other state-of-the-art models that are based on ensembles or that do intelligent sampling. We refer the reader to the main paper for a detailed quantitative comparison of the work, and here we show qualitative results.

The method is very data efficient. The entire training happens within 70 epochs, and we reach SOTA results within the first 40 epochs. Note that most of the other methods require hundreds of epochs to converge. Additionally, we compare the training time with Proxy-NCA (one of the fastest method in the literature) with our method showing a significant speedup for epoch. Finally, in the paper we present a detailed robustness analysis of the method, while in supplementary material we show that our method overfits less than the other methods, introducing an implicit form of regularization.