Authors: Peter Ochs, Tim Meinhardt, Laura Leal-Taixe, Michael Moeller
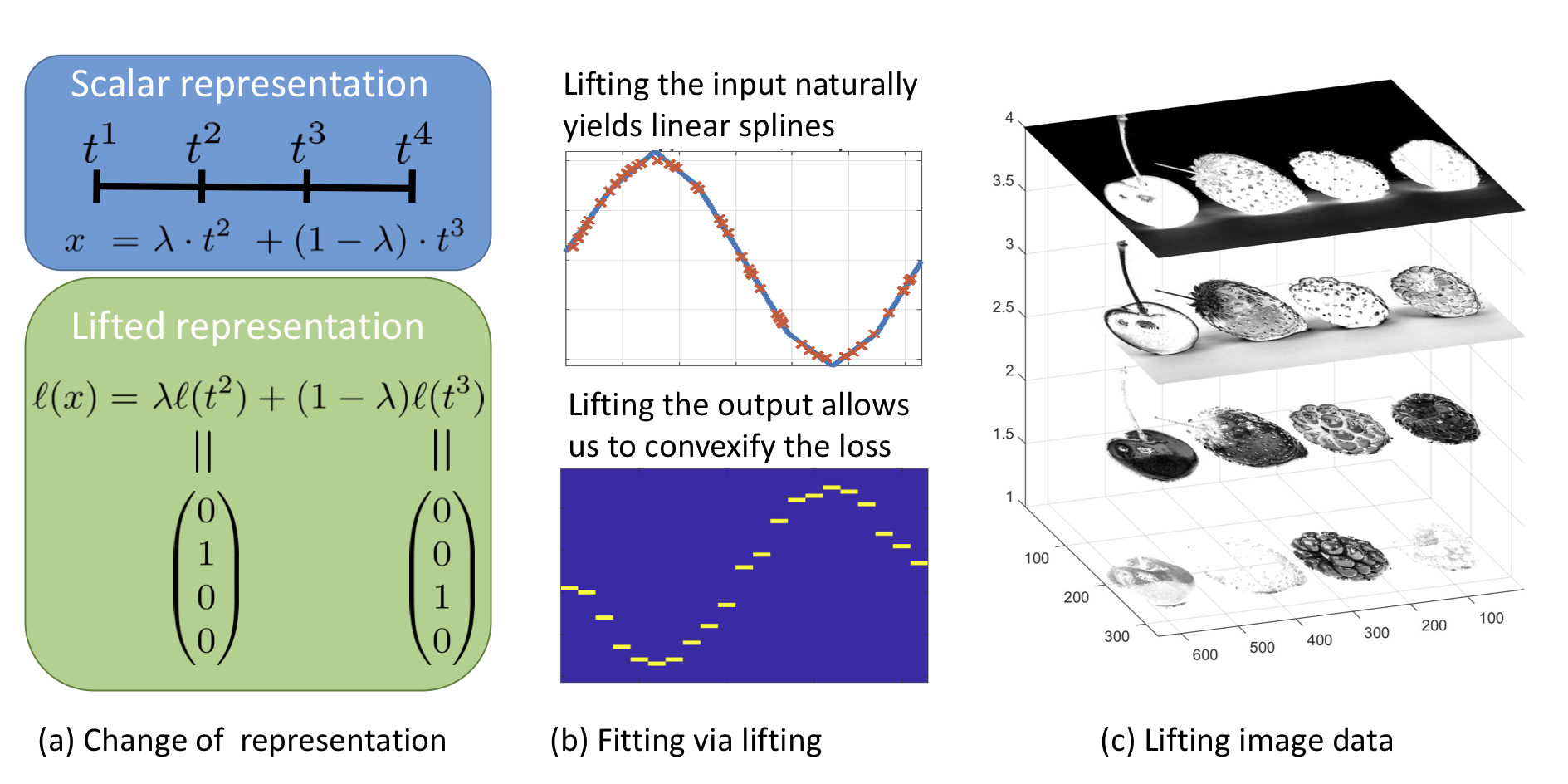
Abstract: The great advances of learning-based approaches in image processing and computer vision are largely based on deeply nested networks that compose linear transfer functions with suitable non-linearities. Interestingly, the most frequently used non-linearities in imaging applications (variants of the rectified linear unit) are uncommon in low dimensional approximation problems. In this paper we propose a novel non-linear transfer function, called lifting, which is motivated from a related technique in convex optimization. A lifting layer increases the dimensionality of the input, naturally yields a linear spline when combined with a fully connected layer, and therefore closes the gap between low and high dimensional approximation problems. Moreover, applying the lifting operation to the loss layer of the network allows us to handle non-convex and flat (zero-gradient) cost functions. We analyze the proposed lifting theoretically, exemplify interesting properties in synthetic experiments and demonstrate its effectiveness in deep learning approaches to image classification and denoising.